Развитие интуиции в математике

Перед вами перевод статьи Калида Азада, автора проекта Better Explained. Статья посвящена тому, как перестать бояться математики и почему традиционное преподавание этого предмета не приводит к пониманию сути вещей.

Автор уверен: математика – это идеи, а кажущиеся сложными формулы – лишь одно из выражений этих идей. Важно найти отправную точку в реальном мире, чтобы затем двигаться дальше, углубляя понимание и знания. Осязаемое воплощение понятий, которое применяется при изучении математики в методе Монтессори, – один из способов развить математическую интуицию. Как объяснять математические идеи так, чтобы они были понятны даже ребёнку? Как можно объяснить что-либо ребёнку, если не понимаешь сам? Рассуждаем вместе с автором, – прим. редакции.

Что такое интуиция в математике

То, как нам преподнесли идею изначально, формирует нашу интуицию. А она, в свою очередь, влияет на то, сможем ли мы наслаждаться предметом. Что же я имею в виду?

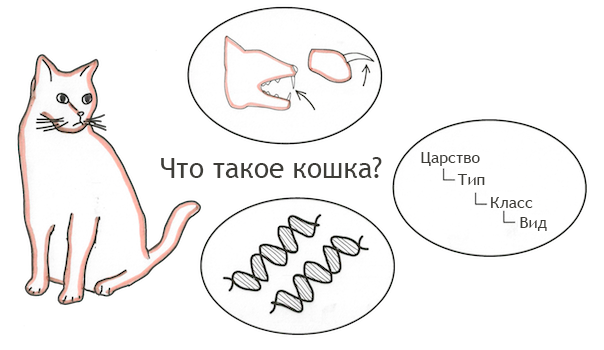
Предположим, что мы хотим дать определение слову «кошка»:

• определение пещерного человека: пушистое животное с когтями, зубами, хвостом, четырьмя лапами, которое мурлычет в моменты счастья и шипит, когда сердится…
• эволюционное определение: млекопитающее, принадлежащее определенному виду (Felis catus), обладающее некоторыми общими характеристиками с другими представителями вида…
• современное определение: вы называете это «определениями»? Кошки – это животные, ДНК которых имеет вид: AЦATAЦATAЦATAЦAT…

Современное определение, конечно, очень точное. Но лучшее ли оно? Дадите ли вы это определение ребёнку, который впервые видит это слово? Даёт ли оно лучшее представление о «кошачести» животного? Нет. Современное определение полезно, но только когда ты уже знаешь, что такое кошка. Это точно не то, с чего стоит начинать.

К сожалению, преподавание математики пока похоже на определение кошки через её ДНК. Нам преподаётся современное, строгое определение, а не идеи, которые привели к нему. Мы остались с загадочными формулами (ДНК), суть которых мы не понимаем.

Давайте рассмотрим идею под другим углом. Представим себе круг: в центре изучаемая идея, а по внешней стороне факты, описывающие её. Мы начинаем с одного факта и следуем по окружности, чтобы развить наше понимание.

Кошки имеют общие физические черты.

А значит:

Кошки имеют общего предка.

А значит:

Вид можно определить совпадением участков ДНК.

Точно! Теперь я вижу, как современное определение было выведено из «определения пещерного человека».

Но не любой факт о предмете может быть использован как отправная точка для рассуждения: значимость этих фактов не одинакова. Правильная перспектива приводит к правильному пониманию – математический первооткрыватель смотрел на вещи под углом, приведшим к озарению.  Поэтому давайте научимся тренировать нашу интуицию.

Что такое круг?

Время для примера из математики: какое определение вы дадите слову «круг»?

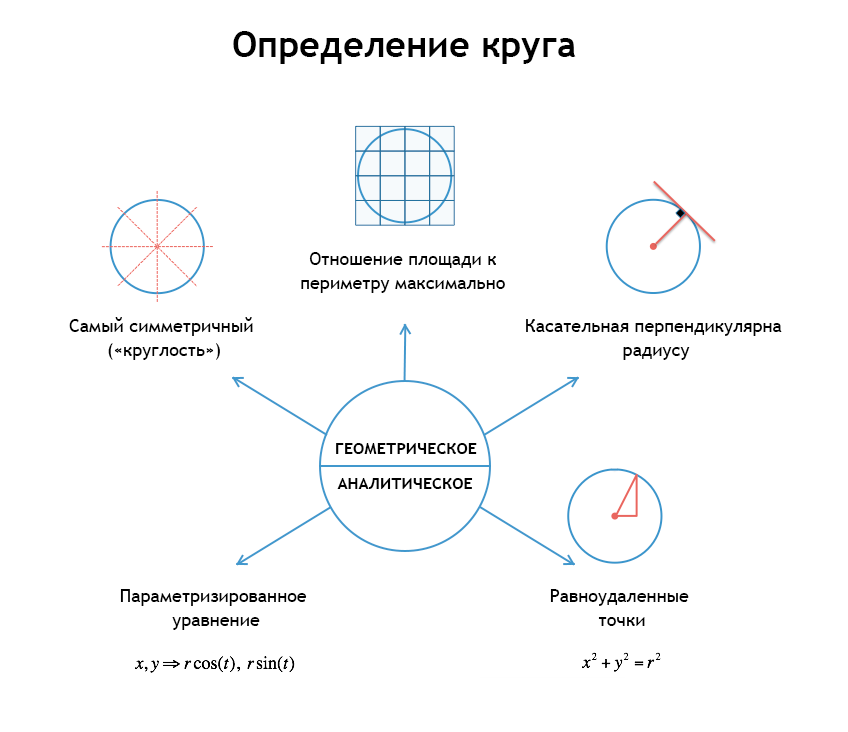
Определение круга

Есть, казалось бы, бесчисленное множество определений. Вот некоторые из них:

Геометрические:

• наиболее симметричная из возможных двухмерная фигура;
• фигура, в которой отношение площади к периметру максимально;
• фигура, в которой касательная линия всегда перпендикулярна опущенному в точку касания радиусу;
• все точки на плоскости, равноудалённые от заданной точки (нанесённые с помощью циркуля).

Аналитические:

• точки (х, у) в уравнении х² + у² = r² (аналитическая версия геометрического определения);
• точки в уравнении r*cos(t), r*sin(t), для всех t.

Этот список можно продолжить, но смысл вот в чём: все факты описывают одну и ту же идею! Это просто разные названия для одной идеи, так же, как 1, один, uno, eins, «решение уравнения 2x + 3 = 5» или «количество носов на лице».

Но все эти первоначальные описания важны – они формируют нашу интуицию. Потому что мы видим круги в жизни, прежде чем увидеть их в классе, и мы понимаем их округлость. Независимо от того, насколько замысловатое, на первый взгляд, уравнение нам покажут (х² + у² = r²), мы уже глубоко внутри самих себя осознаём, что круг – круглый. Если мы изобразим уравнение в виде графика и получим квадрат или кривую линию, мы поймём, что допустили ошибку.

В детском возрасте мы знакомимся с кругом, давая ему определение пещерного человека: «действительно круглый предмет», что обеспечивает нам уверенность и даёт основание для интуиции. Каждая точка на нашем круглом предмете находится на одном и том же расстоянии от центра. Уравнение х² + у² = r² является аналитическим способом выражения этого факта, используя теорему Пифагора. Мы начали с одного факта и с помощью нашей интуиции проработали путь к формальному определению.

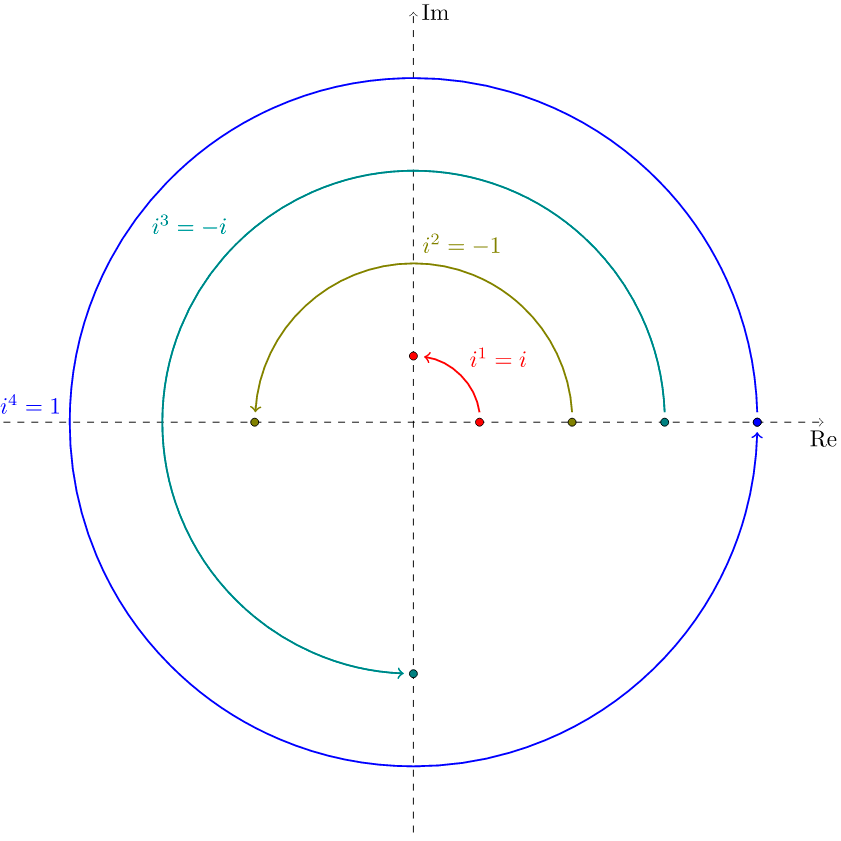
С другими идеями всё гораздо сложнее. Можем ли мы, опираясь на свою интуицию, буквально представить величину «e», или это для нас нечто абстрактное? Понимаем ли мы геометрическую интерпретацию мнимого числа, или это искусственная, бесполезная идея?

Стратегия развития интуиции

Я до сих пор напоминаю себе о глубоком значении величины «е» и мнимого числа – что кажется столь же абсурдным, как и не забывать о том, что круг круглый или как выглядит кошка! Стоит всегда начинать с естественной интуиции, изучая понятие.

Если у меня нет понимания общей картины, это сводит меня с ума: математика – это идеи, а формулы – просто способ выражения идей. Как только приходит понимание основной идеи, уравнения встают на своё место. Вот стратегия, которая помогла мне:

Шаг 1: Найдите центральную идею математической концепции. Это может показаться непростым, но попробуйте начать с её истории. Где идея была впервые использована? Чем занимался её первооткрыватель? Её использование в прошлом может отличаться от нашей современной интерпретации и применения.

Шаг 2: Объясните какое-либо свойство/факт, используя идею. Используйте идею, чтобы провести связь явления или свойства с формальным определением. Если вам повезёт, вы сможете перевести математическое уравнение (x² + y² = r²) в простое словесное определение («Все точки на одинаковом расстоянии от центра»).

Шаг 3: Исследуйте связанные свойства, используя ту же идею. После того, как у вас появится аналогия или интерпретация, которая работает, смотрите, относится ли она к другим свойствам. Когда-то да. Когда-то нет (и вам нужно заново проанализировать ситуацию), и вас ждёт множество удивительных открытий.

В чём же мораль?

На уроках математики мы часто начинаем с последней, самой сложной идеи. И совсем не удивительно, что мы запутываемся, – показываем ДНК и ждём от учеников, что они увидят кошку.

Вот несколько принципов, которые для меня находятся в основе того, как я понимаю и объясняю математику:

1. Ищите идеи и применяйте их. Первая пришедшая на ум мысль поможет поставить всё на своё место. Начните с определения, которое имеет смысл, и идите по кругу, чтобы найти другие.
2. Развивайте терпение и стойкость. Биться головой об идеи не очень весело. Если понять смысл не получается, подойдите к решению с другой стороны. Всегда есть другая книга, другая статья, другой человек, который объяснит это таким образом, что вы поймете смысл.
3. Не бойтесь визуализировать предметы. Мы думаем о математике как жёсткой и аналитической дисциплине, но визуальные интерпретации никто не запрещал! Делайте то, что разовьёт ваше понимание. Мнимые числа сбивали с толку, пока не появилась их геометрическая интерпретация – спустя десятилетия после их первоначального открытия. Нельзя просто смотреть на уравнения день ото дня в надежде получить результат.

Математика становится трудной, когда мы предпочитаем определения пониманию. Помните, что современное определение является наиболее продвинутой стадией мысли, но не обязательно отправной точкой. Не бойтесь подойти к концепции с абсурдной мысли – за любым уравнением есть привычная нам идея на простом языке. Удачи в математике!

Бесплатные уроки от экспертов

Помогут сделать первый шаг в создании развивающего пространства для вашего ребёнка дома